The professional activity that the cardiovascular surgeon performs is much more than a simple gesture to mechanically operate the patient's heart. There is in every act of intraoperative most notions of physiology and physics than we generally realize. This paper discusses, in the light of mathematics, on the dynamics of fluids, ie blood, focused on invasive measurements of blood pressure, the effect of vessel size on its internal resistance and the flow passing through it in conversion of various units of measurements of pressure and resistance, blood viscosity and its relationship to the vessel, hemodilution, differences in laminar and turbulent flow, velocity and blood pressure and wall tension after a stenosis and the origin of poststenotic aneurysm. This study is not to enable the reader to the knowledge of all physics, but to show it as a useful tool in explaining phenomena known in the routine of cardiovascular surgery
A atividade profissional que o cirurgião cardiovascular executa é muito mais do que um simples gesto mecanizado de operar um coração doente. Há em cada ato do intra-operatório mais noções de fisiologia e física do que geralmente nos damos conta. O presente trabalho discorre, à luz da matemática, acerca da dinâmica dos fluídos, ou seja, do sangue, com enfoque nas medidas invasivas de pressão arterial, do efeito do diâmetro do vaso sobre sua resistência interna e do fluxo que passa por ele, na conversão de diversas unidades de medidas de pressão e resistência, viscosidade sanguínea e suas relações no vaso, hemodiluição, diferenças de fluxo laminar e turbulento, velocidade e pressão do sangue e a tensão da parede após uma estenose e a origem do aneurisma pós-estenótico. O objetivo do trabalho não é de habilitar o leitor no conhecimento da física, mas apresentá-la como ferramenta útil na explicação de fenômenos conhecidos na rotina do cirurgião cardiovascular.
INTRODUCTION
"The heart is the only organ of all organs that can not endure injury. This is expected because when the main power source is destroyed, no additional force can be brought by the organs that depend on it" (Aristotle-384 BC).
These words of Aristotle strongly rumble in the history of the specialty called "cardiovascular surgery". Patients with lacerations of the heart, terminal heart failure, cardiac cachexia, congenital heart disease, myocardial infarction and recurrent acute pulmonary edema surrendered to the surgeon's scalpel in an attempt to avoid the inevitable fate: death.
Often, these fearless surgeons had no success in the fight against the sharp scythe of death, causing fear, distrust and even bans on the continuity of the "art of healing" by the population or, worse still, of professional colleagues.
However, with much effort and persistence, the surgical techniques have been consolidating, changing the outcome of the sad end of the patient with heart disease. Names such as Le Gallois, Alfred Blalock, Lillehei, John Gibbon, Kirklin, Christian Barnard, Euryclides Zerbini, Adib Jatene, Domingo Braile, to mention a few, have become icons in cardiac surgery.
The advancement of techniques was only possible through knowledge of anatomy, physiology and dynamics of circulation, making every cardiac surgeon a scientist, a potential physiologist, providing him the ability to formulate new "answers", new techniques for solving cardiac problems [1-3].
Aristotle was right when he said no organ would support the failing heart on its deathbed, however, he did not predict that the deep knowledge of the circulatory dynamics could provide a new life for the patients considered, until recently, as terminals.
The aim of this study, which will be didactically divided into two parts, will be to briefly discuss topics of routine cardiovascular surgeon, in the light of physics, with respect to circulatory and gas dynamics.
HYDROSTATIC
Hydrostatic pressure is the force exerted by a fluid across a surface of unit area.
a) The pressure exerted by a fluid at a given point is equal in all directions from this point;
b) The pressure exerted in points in the same horizontal plane are equal;
c) The pressure exerted by a fluid increases linearly with depth.
Mathematically, the pressure is expressed by equation (EQ) I:
EQ I: P = pressure (Pa), p = density (kg/m
3), h = height (m) g = acceleration due to gravity (m/s
2)
Note: g = 9.8 m/s
2
Figure 1A shows common circuit of pressure measurement performed with a combination of a liquid column manometer (extensor) and a pressure transducer. The extensor is postitioned with one side to the patient (artery, usually radial), and another to the transducer to measure pressure. When we raise the operating table without raising the pressure transducer, we have the situation represented by Figure 1B, where the pressure is overestimated as a result of higher compression of the membrane of the measuring circuit, which causes incorrect measurement. Figure 1C shows the situation of lowering the operating table, leaving the pressure transducer positioned above the patient, which underestimates arterial pressure.
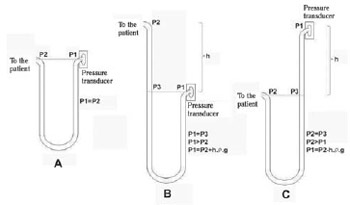
Fig.1 - A. Pressure measurement circuit with end available to the pressure transducer and to the patient on the same level. B. End of the transducer positioned lower than the patient. C. End available to the patient positioned lower than the pressure transducer (P = pressure, h = height, ñ = liquid density, g = acceleration due to gravity).
The pressure transducers shown in Figures 1A to 1C are electrical transducers known as a Wheatstone bridge, whose schematic symbol is shown in Figure 2. In this type of instrument, pressure is applied on a membrane, which is connected to a set of electrical resistances. Usually there are two fixed resistors and two variable ones arranged in diagonal position and their degree of deformation caused by compression of the membrane results in the reading of a different value of electric current (Figure 2). This variationof current is amplified and calibrated with standard devices (equipment) so that the manometer serves to measure the pressure. The pressure now converted into electrical voltage can be displayed, stored and recorded graphically [4,5]. Its features are as follows:
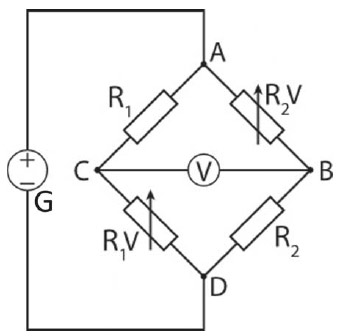
Fig. 2 - Basic scheme of Wheatstone bridge, used in simpler pressure transducers. A, B, C, D = intersection points of the circuit, G = generator V = Voltmeter, R1, R2 = fixed resistors; R1V, R2V = variable resistors.
a. The pressure variations are measured with minimal variations in volume of the transducer cavity. These are limited to that necessary to deform the membrane. In the liquid column manometer, pressure variations are measured at the expense of a displacement of the liquid column, whose magnitude depends on the density of the liquid used. The variation in volume of this column by the pressure is always high, and may, in certain circumstances, affect the own pressure to be measured;
b. The inertia of the liquid column is much larger than the transducer's membrane. The result is that the liquid column manometer is not able to record rapid variations in pressure, while the pressure transducer is able to record about 100 cycles per second.
This inertia of the water column contained in the circuit makes it less sensitive to reproduce perfectly the nuances of the pressure curve [6].
An ideal circuit is one that the pressure transducer is at the same level as the patient's heart and with the smallest distance and amount of fluid between the pressure transducer and the patient [6].
Table 1 shows the different factors for converting pressure in its different units. For example, when we want to convert 1.0cmH
2O into mmHg, one should just multiply it by 0.74, because mercury is approximately 13.6 times more dense than water. So, to convert cmH
2O into mmHg one should just divide by 1.36 or multiply by 0.74.
HYDRODINAMIC
Fluids are substances that are incapable of preserving their form in the presence of a shear force. However, everyone knows that the fluid resists to certain changes of form. At a time when the shear force acts to displace a liquid layer on another, adjacent, there is a force of cohesion between the layers, which opposes this movement. This cohesion, which is a form of internal friction between layers of fluid is called viscosity [6].
In practical terms, the viscosity causes resistance to flow inside a cylindrical tube, leading to the formation of concentric layers of decreasing speeds of the center (maximum speed) to the periphery (zero speed). These layers prevent the mixing of elements between layers. So, they are responsible for flow laminarity [6].
LAMINAR FLOW IN THE INTERIOR OF TUBULAR CONDUCTORS
For flow to occur, there must be pressure gradient (EQ II) along the tube (Figure 3).

Fig. 3 - Laminar flow inside a cylindrical tube. Note that the flow is determined by the pressure gradient, and that each flow ring has its own velocity, thus causing internal friction (viscosity) between the various layers of liquid in motion. Modified from Silva Jr MR. Fisiologia da circulação. 2
a ed. São Paulo:Edart;1977. p.9.
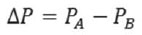
EQ II: PA = pressure at point A, PB = pressure at point B, but as we are working with tubular conductors, the difference in pressure ratio is given by EQ III:
EQ III: d = distance from point A to point B.
It can be shown that if a tube has radius R, the flow velocity of a liquid ring situated at a distance "r" from the axis is given by EQ IV:
EQ IV: Vr = velocity of the liquid measured at a distance "r" from the center of the tube; Vmax = maximum velocity of the liquid inside the tube, R = tube radius, r = distance up to the center of the tube.
Thus, when r = R, Vr = 0 and when r = 0, Vr = Vmax.
As Vr grows as a function of the "r" square, the velocity profile inside a tubular conductor is parabolic, as shown in Figure 3.
The maximum velocity within a conductor tube is given by EQ V:
EQ V: n = coefficient of viscosity.
The flow equation for each ring of radius "r" is given by EQ VI:
(EQ VI) These elements lead to determining the contribution of each full flow ring inside the tube. This is done by adding up the flows of each infinitesimal ring or, in mathematical terms, integrating the flow equation (EQ VI), from r=0 (center of the tube) to r=R, as follows:
And by EQ IV, we have:
Hence follows the EQ VII:
(EQ VII) which shows us that the flow depends directly on the radius of the tube and the velocity of the fluid inside it. Applying the EQ V to EQ VII, we have:
and, applying the EQ III to EQ VIIa, we have the EQ VIII:
(EQ VIII) which is called the Hagen-Poiseuille equation. Through this equation, we note that the flow is inversely proportional to the length of the tube and the viscosity and directly proportional to the fourth power of the radius and the pressure difference between the ends [6]. Thus, in one coronary artery with atherosclerosis with 50% decrease of its diameter, the flow passing through it will be decreased by 94% (since the arterial pressure and blood viscosity are preserved).
HYDRAULIC RESISTANCE
For a given tubular conductor and a liquid of known viscosity, the Hagen-Poiseuille equation shows that there is a constant relationship between flow and pressure, or that is, that the flow is a linear function of ΔP. The relationship ΔP/F is called Rh hydraulic resistance. When dividing EQ II by EQ VII, we have the EQ IX:
(EQ IX) Here, resistance is directly proportional to the vessel length and inversely proportional to the radius raised tothe fourth power. In the previous example, if we reduce the diameter of the coronary artery by half, its resistance would be increased by 16 times [6].
In the analysis of calculated resistance (pressure/flow) there are various units often used, depending on the units of flow and pressure, but two highlight, which are: Wood and dynas.s.cm-5 units. The conversion from one unit to another is developed in the calculations below:
(EQ X), thus
(EQ XI), where µ
x is the unit of X.
But for converting Wood to dynas.s.cm for
-5, we have:
and then
But
(EQ XII),
(EQ XIII) and
(EQ XIV) Applying the EQ XII, XIII and XIV in X, we have:
(EQ XIV)
To calculate the peripheral vascular resistance we will replace values to EQ X. When creating a hypothetical situation in which the mean pressure measured in the upper limb of an adult is 70 mmHg and his cardiac output (flow) of 5 L/min, we have:
Similarly, we can calculate pulmonary resistance, assuming a mean pressure of 20 mmHg and flow (flow) of 5 L/min:
The normal range of systemic vascular resistance is 11 to 18 Wood or 900 to 1400 dynas.s.cm-5 and pulmonary vascular resistance, 1.9 to 3.1 Wood or 150 to 250 dynas.s.cm
-5. Here I must make one important exception: the pressure that we previously mentioned is the effective pressure. It is real only when the central venous pressure (in the case of systemic resistance) or the left atrial pressure (in the case of pulmonary vascular resistance) is zero. If it is not, one should just subtract the pressure measured in systemic or pulmonary artery by the pressure obtained by the central venous line or left atrium, respectively, before we divide by the flow (which is the cardiac output) [7].
SETS OF HYDRAULIC RESISTANCE
If
n hydraulic conductors are placed in series, the total R
h (resistence) of the system is the sum of individual resistances.
(EQ XV) If the conductors are arranged in parallel, the sum of the inverses of the individual hydraulic resistances is equal to the inverse of the total hydraulic resistance.
(EQ XVI) In the circuit in series, F (flow) is equal to all resistances (EQ XV), while in parallel circuit, ΔP (pressure gradient) is equal to all resistances (EQ XVI).
In the circulatory system, we have a complex combination of hydraulic resistances in series and in parallel. Basically, however, we can affirm that the circuit consists of a sequence of segments in series (arteries, arterioles, capillaries, venules and veins), each segment, in its turn,consistis of a set of vessels of geometry approximately equal, arranged in parallel, irrigating the different organs (Figure 4).

Fig. 4 - Illustration of the properties of hydraulic resistors in the circulatory system: A, B, C, D, E represent successive segments of a vascular system (artery, arteriole, capillary, venule, vein, respectively). The elements of a segment are resistors in parallel. The segments, in turn, are disposed as resistors in series. From Silva Jr MR. Fisiologia da circulação. 2ª ed. São Paulo:Edart;1977. p.11.
The principles of hydrodynamics described above apply strictly to the Newtonian fluids, or that is, homogeneous fluid of not too high viscosity, flowing with laminarity inside cylindrical tubes of rigid walls. The flow under certain conditions can switch from laminar to turbulent, but in almost all physiological situations the blood flow into the vascular system is laminar. However, the principles of hydrodynamics does not apply strictly to the blood due to two reasons:
1. Blood vessels are not rigid tubes, but elastic and active, or that is, they can undergo changes in their geometry and these changes can be passive, by forces applied to the walls or active by the action of smooth muscle of these walls.
2. Blood can not be considered a Newtonian fluid. We will note that the main factor of anomaly in the behavior of blood as a Newtonian fluid is the presence of red blood cells.
Blood is an aqueous solution of salts and proteins containing red blood cells in a ratio of approximately 35- 40% (hematocrit). Blood viscosity depends on the following factors:
a.
Influence of hematocrit: Blood viscosity increases exponentially with increasing hematocrit. For the normal hematocrit, blood viscosity is about four times higher than water viscosity (n water = 1);
b.
Influence of temperature: The viscosity of any fluid varies inversely with temperature. Blood viscosity increases about 2.5 times when the temperature decreases from 37ºC to 0ºC. This variation is parallel to the water viscosity, so that the relative blood viscosity (defined by relationship çblood/n H
2O at a given temperature) is nearly constant.
c. Blood viscosity in very thin tubes: The
Fahraeus- Lindqvist effect (Figure 5) shows that the smaller the vessel diameter, the smaller will be the viscosity of the liquid contained therein.
Fig. 5 - Fahraeus-Lindqvist effect: viscosity of blood, normal hematocrit, measured in glass viscometers of variable radius. For radius larger than 1 mm, blood viscosity is constant. For smaller radius, the viscosity decreases due to the decrease of the radius. From Silva Jr MR. Fisiologia da circulação. 2ª ed. São Paulo:Edart;1977. p.17.
This effect can be explained as follows: when we deduce the
Hagen-Poiseuille equation (EQ VIII), we use the integral of the flow equation (EQ VI). Integration is supposed to be the sum of an infinite number of infinitesimal portions, which is the situation that occurs with the flow rings in a Newtonian fluid. But when blood flows through terminal arteries, whose radius is about 600 ìm or arterioles (20µm), capillaries (7µm), venules (30µm), or terminal veins (1,500 ?m), the size of red cell (7µm) is close to the actual vessel diameter. It is no longer possible to integrate the equation of velocity and are no longer applicable to the Hagen- Poiseuille equation;
d.
Axialization of red blood cells: When the blood moves within a tubular conductor, the red cells tend to accumulate in the axis of the tube, leaving a marginal plasma zone virtually free of red blood cells. It results in presence of vascular branches with very low blood hematocrit. An example is the blood that is collected by superficial puncturing of the skin which has hematocrit about 25% lower than the blood collected from a large vein in the same individual [6].
THE HEMATOCRIT AND THE HEMODILUTION
The hematocrit (Ht) is presented in percentage (%) andis a relationship between two volumes: the packed cell volume and total volume, as shown in equation XVII [7-10].
(EQ XVII) When we introduce a volume (prime) with crystalloid solution (lactate Ringer's or saline solution) the final hematocrit (HTf) changes, according to the formula:
(EQ XVIII) but, according to EQ XVII
(EQ XIX) The packed cell volume is a sum of erythrocytes and platelets, and erythrocytes account for more than 95% of this total. So, we disregard the involvement of other cellular constituents. When replacing EQ XIX by XVIII, we have:
(EQ XX) To consider all the factors as a function of blood volume, we calculate how much this prime corresponds to such volume:
(EQ XXI) and "x" is how much the prime represents the patient's blood volume.When replacing EQ XXI by EQ XX, we have:
(EQ XXII) When we simply "blood volume", we have:
(EQ XXIII) Thus, we prove that the final hematocrit is equal to the initial hematocrit divided by 1 plus how much the prime represents the initial blood volume.
In practice, to apply the XXIII equation we should imagine a patient with a blood volume of 4 liters of blood and hematocrit of 40%, who had undergone hemodilution with 1000 ml of crystalloid solution (1000 ml represent 0.25 of patient's blood volume and Ht = 40% is actually 0.40).
When applying the formula:
Thus, the final hematocrit will be 32%.
TURBULENT FLOW
All the aforementioned considerations refer to the laminar flow situation, or that is, on which the various flow rings move sliding over each other without mixing. If, however, the radius of the tube increases, a point on which the flow ceases to obey the
Hagen-Poiseuille equation (EQ VIII) is reached. If we make a graph of velocity as a function of pressure (Figure 6), we will note that there is a point on which the inclination of the straight decreases, indicating therefore that there was an increase in hydraulic resistance.
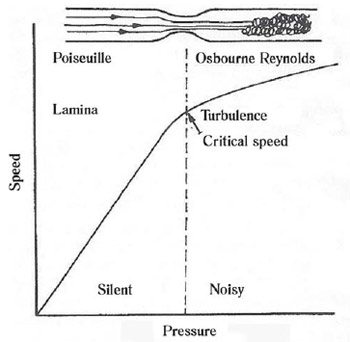
Fig. 6 - Changes in flow, when it goes from laminar to turbulent. From Silva Jr MR. Fisiologia da circulação. 2ª ed. São Paulo:Edart;1977. p.29.
The English engineer Osbourne-Reynolds has shown, in the middle of last century that from the point on which there is the abrupt change in hydraulic resistance, the flow ceases to be laminar and becomes turbulent, or that is, there is mixing between fluid adjacent blades. Increased resistance is due to the fact that the energy dissipated in the system increases. In laminar flow, the energy is dissipated solely to overcome the viscosity of fluid between adjacent blades in motion, whereas in turbulent flow, part of the energy is dissipated into kinetic energy, which moves the liquid lateral waves.
Thus, the relationship between flow and pressure is no longer determined by the Hagen-Poiseulle equation. The stenosis of an arterial segment suddenly increases vascular resistance, which makes the flow turbulent, leading to formation of a subsequent dilation (we will show at the end of the article), which sharply decreases vascular resistance, making the flow more turbulent [6].
BERNOULLI'S PRINCIPLE
The relationship between velocity and pressure exerted by a fluid in motion is described by the Bernoulli's principle: when the velocity of a fluid increases, the pressure exerted by the fluid decreases.
Bernoulli's formula is:
EQ XXIV: P = pressure (mmHg), r = density (g/cm
3), g = acceleration due to gravity (9.8 m/s
2) h = height (m).
When accepting ha = hb, we can subtract in both members ñgh, leaving only:
(EQ XXV) Thus, we conclude that pressure and velocity measurements are inversely proportional [6:11-13]. The practical example will be given after presentation of the Laplace's Law.
LAPLACE'S LAW
Imagine the blood flow in a blood vessel that has a certain radius and a known thickness. The vessel wall is compressed as a result of pressure of liquid contained therein. Laplace's Law describes the relationship between the transmural tension, pressure, radius and thickness of the vessel wall. Obviously, the higher the pressure inside the vessel, the greater will be the tension of the wall. Otherwise, the thickening of the vessel decreases its transmural tension. Also, the larger the radius, the greater the tension. Mathematically, we have:
EQ XXVI: T = wall tension (in mmHg), P = pressure inside the vessel (in mmHg), R = radius of the vessel (in mm), M = wall thickness (in mm).
Figure 7 illustrates the effect of the radiun on the surface tension of the balloon, since as the Pascal's principle the pressure inside the balloon is the same, irrespective of location, radius or orientation of the balloon.
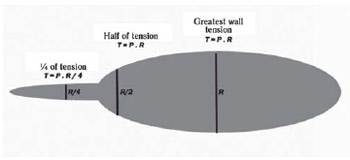
Fig. 7 - Balloon that exemplifies the Laplace's Law. The principle of Pascal says the pressure is the same at all points of the balloon, but there is great difference in wall tension in different parts of the balloon. These variations are described by the Laplace's Law. T = wall tension, P = pressure, R = radius of the balloon
The knowledge of Bernoulli's principle and the Laplace's law are critical when we seek an explanation for the effect of poststenotic dilatation. At the site of stenosis, the radius of the vessel is reduced. Because the flow is constant and depends directly on the blood velocity and the radius of the vessel (EQ VII), the velocity will increase. When leaving the site of stenosis, the flow moves to a region with larger diameter. So, again using the EQ VII, we conclude that the flow will slow down, causing increased blood pressure at the site (
Bernoulli effect). This increase in pressure will increase the surface tension in this segment of the vessel (
Laplace's Law), causing the dilation. Increasing the diameter of the vessel not only further increases wall tension (
Laplace Law), as further slow down the blood flow, thus greatly increasing its pressure (
Bernoulli effect). This evolution of the vessel lumen only ends when it becomes torn or surgically corrected (stenosis and dilation)[14-18].
Despite the Laplace's Law to be very useful in practice, it presents some problems. In the equation, the vessel is considered a massive structure, or that is, consisting entirely of solid material, which is not true. About 70% of the vessel wall is composed of substances in liquid form. It is not our objective to approach the issue deeply, but we can point herein an indication of a study that shows a formula that better reflects the reality of the vessel wall: Quick CM, Li JKJ, Weizsacker HW, Noordergraaf A. Laplaces law adapted to a blood vessel with two-phase wall structure. Acessed on 17/08/08. http://ieeexplore.ieee.org/iel3/3907/11337/00513710.pdf [19].
BLOOD STASIS OF THE ANEURYSM
When the angle of expansion of the vessel (Figure 8) is equal to or greater than 7 degrees, laminarity is disrupted, creating a vortex region, which in circulatory dynamics mean turbulence and hence formation of thrombus [12]. The determination of this angle can be easily obtained with measurements with echocardiogram or ultrasound with or without Doppler, as illustrated in Figure 9 and in EQ XXVII:

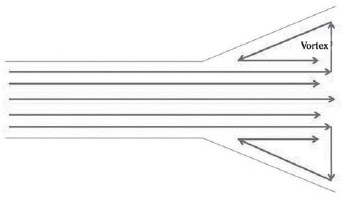
Fig. 8 - Schematic diagram of the flow within an aneurysm, with the formation of vortex

Figure 9 - Schematic diagram of the aneurysmal vessel and its ultrasound measures. Such measures are important for determining the angle of the aneurysm. a = angle of expansion of the vessel. A: smaller vessel diameter, B: distance measured in the vessel wall between its normal diameter and its largest expansion, C: larger vessel diameter
EQ XXVII: α-angle of expansion of the vessel, A-minor diameter of the vessel; B-distance measured in the vessel wall between its normal diameter and its largest dilation, Clargest vessel diameter.
And with the development of the previous equation, in the equation XXVIII we find the determination of the alpha angle of the dilation.
CONCLUSIONS
Understanding how the inner shape of a vessel influences the velocity and flow of blood passing through the aorta, coronary arteries or any vessel in the body, how a vessel that becomes aneurysmatic tends to increase, independent of other external factors, how blood clots are easily found in aneurysms - and associated with this cerebral ischemic events; how blood viscosity behaves in relation to hematocrit, temperature and capillaries; how resistance affects the flow and blood velocity as well as how to exchange some pressure units initially seems task of a scientist.
However, the cardiovascular surgeon is historically a scientist. The practice of our specialty with all its surgical and mechanical support technique was and is only possible by applying the acquired knowledge in physiology and physics. The disclosure of this knowledge is essential so that their experts will continue producing new techniques and equipment that will be useful for the specialty and, ultimately, to patients themselves. In another study the gas dynamics and its relation to cardiovascular surgery will be approached.
ACKNOWLEDGEMENTS
We thank Dr. Maurício Rocha e Silva Jr., for having kindly provided the rights of reproduction in Figures 3 to 6.
1. Braile DM, Godoy MF. História da cirurgia cardíaca. Arq Bras Cardiol. 1996;66(1):329-37.
3. Prates PR.: Pequena história da cirurgia cardíaca: e tudo aconteceu diante de nossos olhos... Rev Bras Cir Cardiovasc. 1999;14(3):177-84. View article
5. Ziaie B, Wu TW, Kocaman N, Najafi K, Anderson DJ. An implantable pressure sensor cuff for tonometric blood pressure measurement. Acessado em 17/08/2008. Disponível em: http://www.eecs.umich.edu/najafi/pdf/Paper_88.pdf
6. Silva Jr MR. Fisiologia da circulação. 2ª ed. São Paulo:Edart;1977. p.1-35.
7. Knobel E. Terapia intensiva pediátrica e neonatologia. 1ª ed. São Paulo:Atheneu;2005. p.283-92.
8. Princípios Éticos na Experimentação Animal. Colégio Brasileiro de Experimentação Animal - COBEA.
10. Zlochevsky ERM, Paes LSN, Imperial MCG, Rios MBS.Índices, fórmulas, tabelas, gráficos e bulário. In: Matsumoto T, Carvalho WB, Hirschheimer MR, eds. Terapia intensiva pediátrica. 2ª ed. Vol 2. São Paulo:Atheneu;1997. p.1205-318,.
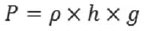




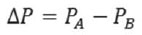
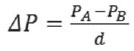


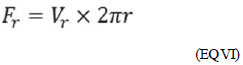

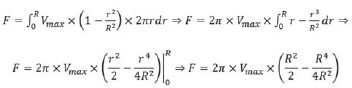
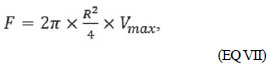


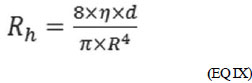

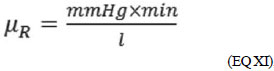
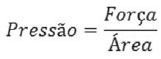
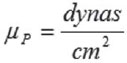

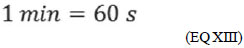
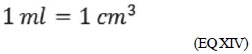
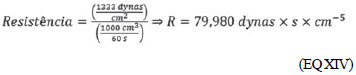
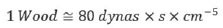
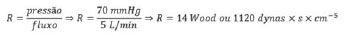
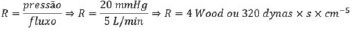

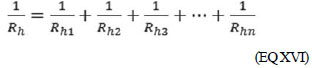




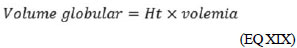
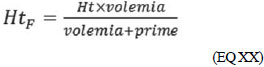
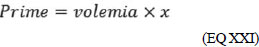

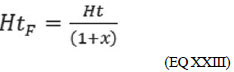


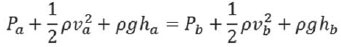
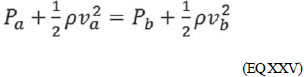
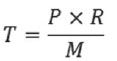




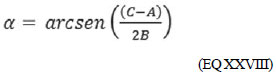
 All scientific articles published at bjcvs.org are licensed under a Creative Commons license
All scientific articles published at bjcvs.org are licensed under a Creative Commons license