OBJECTIVES: To study the influence of geometric factors upon the function of modified Blalock-Taussig anastomoses (mBT) using a computational dynamic code based upon the method of finite elements.
METHODS: The mBT operation, performed in 10 patients, was graphically reconstructed to create a parametric 3-dimensional geometric model. Using Streamline Upwind/Petrov-Galerkin approximations, blood flow and distribution were evaluated in different diameters of subclavian arteries and polytetrafluoroethylene grafts (PTFE) and angles of proximal anastomoses.
RESULTS: The percentage of blood flow derived through the PTFE grows as its diameter increases in relation to subclavian artery diameter. Variations in the PTFE diameter do not interfere with pulmonary artery flow distribution. An angle of 110º in proximal anastomoses results in a high percentage of blood derivation to the graft, while angles of 30º, 60ºand 90º present with almost similar flow rates. However, angles of 30º and 110º produce an excessive flow to one of the pulmonary arteries, in detriment of the other. Peak pressure in the PTFE is affected by the proximal angle of anastomosis, with 30º resulting in higher and 110º in lower values. As the angle increases, the region of higher pressure shifts from the PTFE to subclavian artery.
CONCLUSION: In the experimental model, percentage of flow derived in the PTFE is directly related to the diameter of the graft. The ratio between the diameters of subclavian artery and graft is an important regulator of flow deviation to the anastomosis. Angles of the anastomosis between the subclavian artery and the PTFE of 60º to 90º result in favorable pulmonary artery flow distribution and the location of the peak pressure.
OBJETIVO: Dinâmica computacional foi utilizada para avaliar a influência de fatores geométricos no funcionamento de modelo da cirurgia de Blalock-Taussig modificada (BTm), ou interposição de enxerto de politetrafluoretileno (PTFE) entre as artérias subclávia e pulmonar.
MÉTODO: A cirurgia de BTm, realizada em 10 pacientes, serviu para compor modelo geométrico tridimensional parametrizado, avaliado quanto a diferentes diâmetros de artéria subclávia e PTFE e ângulo proximal da anastomose. Foi empregado o código de dinâmica computacional FLOTRAN baseado no método de elementos finitos conhecido como "Streamline Upwind/Petrov-Galerkin".
RESULTADOS: Nas simulações, a porcentagem de fluxo desviada pelo enxerto aumenta com a relação entre diâmetros do PTFE e da artéria subclávia. Um ângulo de 110º na anastomose proximal mostra maior porcentagem de sangue desviado, enquanto que 30º, 60º e 90º mostram desvios de fluxo quase similares. Contudo, ângulos de 30º e 110º tornam excessivo o fluxo pulmonar em uma das artérias pulmonares, em detrimento da outra. O pico de pressão no PTFE varia conforme o ângulo adotado, sendo maior em 30º . Quando o ângulo da anastomose aumenta, a região de maior pressão se desloca do enxerto para a artéria subclávia.
CONCLUSÕES: No modelo experimental, o diâmetro do enxerto de PTFE é regulador principal da porcentagem de fluxo desviado. Na análise computadorizada, um ângulo de 60º a 90º entre artéria subclávia e enxerto de PTFE parece mais adequado para anastomose, considerando-se percentagem de fluxo desviado, sua distribuição entre ramos pulmonares e pico de pressão na zona da anastomose.
INTRODUCTION
Computer dynamics of fluids are utilized to simulate blood flow with the aim of assisting in research on the treatment of vascular disease [1]. The investigation has collaborated in the understanding of the hemodynamics of the human circulatory system, in the projection of new vascular prostheses and valves and in the perfection of surgical techniques. The simulations of blood flow are concentrated on arteries with bifurcations, branches and bends, in which there is an increased incidence of disease such as arteriosclerosis, aneurysms and thrombosis [2,3,4]. There have been more studies of the carotid, abdominal aorta and anastomosis of vascular grafts in the femoral artery [1,4,5,6].
A surgical technique used to increase the pulmonary flow in patients with pulmonary blood hypoflow due to congenital heart disease is the interposition of a tubular graft of polytetrafluoroethylene (PTFE) between subclavian and pulmonary arteries. The procedure, known as the modified Blalock-Taussig shunt (mBT ) [7], allows redirection of part of the systemic blood flow to the pulmonary arteries, with a consequent clinical improvement and better survival of the patients, as was observed in the original procedure [8,9]. The satisfactory result depends on the increase of pulmonary blood flow and thus, on the dynamics of the flow in the graft and pulmonary arteries, and is directly related to geometric factors recognized during surgery, such as diameters and length of the arteries and the angles of anastomoses [10,11]. A greater comprehension of the relationships between these factors might improve the surgical technique and therefore improve the immediate and late results [12].
In this work we evaluated the influence of different configurations of structures involved in the mBT shunt on the blood flow, utilizing a 3-dimensional parameterized geometric model obtained from surgical procedures and capable of simulating different operative configurations.
METHODS
Patients and medical conduct
Ten patients with congenital heart disease and pulmonary hypoflow who were submitted to mBT-type systemic-pulmonary shunt surgeries in the cardiology Institute of Rio Grande do Sul / Fundação Universitária de Cardiologia, Brazil, from March to July 2001 were included in this study. Their characteristics are described in Table 1.
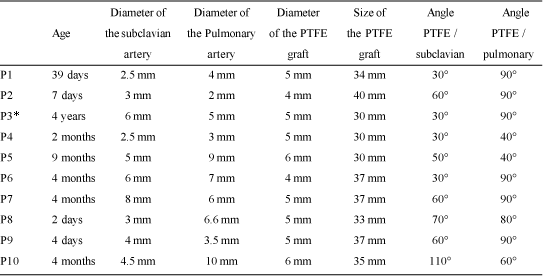
Table 1. Characteristics of patietns with cyanotic congenital heart diseases whose modified Blalock-Taussig surgery served as a model for this study.
Indication for mBT surgery conformed to the criteria of: congenital disease, option of the pediatric cardiologist, clinical condition of the patient and individual preference of the surgeon. The patient was included only if the guardian gave written consent and the Institution's Research Ethics Committee approved the study.
Medical procedures, including preoperative preparation when a color doppler echocardiographic examination was made and the trans-operative and postoperative procedures have been previously described [13]. When performing the mBT-type anastomosis an attempt was made to utilize PTFE grafts of equal sizes or greater than 4 mm (Table 1). On finishing the procedure, the surgeon or the first assistant, made a detailed design of the procedure utilized as basis for the development of the computerized model. The parameters obtained from the patients were the diameters and lengths of the PTFE graft, the subclavian artery and the left pulmonary artery as well as the proximal and distal angles of the anastomosis of the PTFE graft in the arteries. All the patients evolved satisfactorily and hospital release occurred between the 7th and the 12th postoperative days.
Construction of the model
A 3-dimensional parameterized geometric model was developed using the measurements obtained in each surgical procedure. The lengths of the arteries and the PTFE graft were determined from surgical observation, from measurements of the pre-operative echocardiographic examination and from results obtained from pulsating simulations. With the objective of measuring the influence of geometric determinants (the diameter of the vessels and graft, the length of the graft and angle of the anastomosis), simulations in a permanent regime were performed modifying these parameters.
Computational aspects
The simulations were performed in the Applied Fluid Mechanics and Computational Laboratory of the Federal University of Rio Grande do Sul and the National Center of Supercomputation (LAMAC). The computational resources utilized in the numeric simulations were a "Silicon Graphics ORIGIN 200 Workgroup server" - with 2 CPUs and 256 Mb of RAM memory and 4 "Silicon Graphics Octane Workstations" - with 2 CPUs and 128 Mb RAM memory in each machine.
The code of computational fluid dynamics Flotran (Ansys Inc.) was used. The stabilization method of finite elements for advection diffusion problems was adopted baptized as "Streamline Upwind/Petrov-Galerkin"(SUPG) [14-18]. To represent the dominion of integration, the 3-line hexaedric element with 8 nodes was utilized, employing the classical interpolation functions to expand the components of quality of movement and pressure. The elements are denominated as Lagrangean, as functions of shape are formed from the products of Lagrange polynoms (3-linear base functions are products of the unidirectional linear base functions). The scientific visualization program Ensight was utilized to perform the post-processing.
The profile of entry velocity in the subclavian artery was considered uniform in all the simulations in permanent regime. The blood was considered as a Newtonian fluid and the arteries were considered rigid. The condition of pulsating flow in the subclavian artery was obtained from the color Doppler examination performed on a patient previously submitted to the mBT procedure. Circuit conditions defined by Migliavacca et al. [19] in previous studies were utilized in the developed models for a comparative study but they were not included in this study.
It was necessary to determine the optimal lengths of the subclavian artery (Lsubclavian = 152 mm) and the pulmonary artery (Lpulmonary = 40 mm) to be modeled, as seen in Figure 1. For this, the numerical results were compared with the measurements obtained in the aforementioned color Doppler echocardiographic studies.

Fig. 1 - Optimal lengths of the subclavian artery (Lsubclavian = 152 mm) and of the pulmonary artery (Lpulmonary = 40 mm) in the model used for computerized analysis
The employed code solved the system of equations in a segregated manner, suggesting the necessity of links between the variables, specifically between velocity and pressure in incomprehensible flows. The method baptized as SIMPLE ("Semi Implicit Linked Equations") of Patankar & Spalding 1972, was utilized to identify this link. The solution of the system of algebraic equations was obtained utilizing the TDMA line-to-line method ("TriDiagonal Matrix Algorithm") [20].
Results obtained from the analyzed models in respect to the distribution and velocity of the flow are expressed as mean values.
RESULTS
Flow diverted by the graft
It is confirmed that the greater the diameter of the graft the greater is the blood flow diverted to the lungs, as can be seen in figure 2. For any length of the PTFE grafts, the distribution of flow to the pulmonary branches remains constant. It can be seen that the increased blood flow in the graft as its diameter increases is independent of the relationships of the diameters of the subclavian artery and the graft, as is illustrated in figure 3.

Fig. 2 - Mean percentage of the flow redirected by the graft and distributed by the pulmonary arteries, in respect to the diameter of the PTFE graft. The greater diameters correspond ot the higher percentages of flow, where the distribution of the blood to the pulmonary arteries are constant for any particular angle of anastomose

Fig. 3 - Mean percentage of the flow redirected by the graft n respect to the diameter and the ratio between the diameters of the subclavian artery and graft. The flow is favored with a greater diameter of the graft compared to the subclavian artery (ratio greater than 1)
The angle of anastomosis also has a significant influence of the percentage flow diverted by the graft. The percentage of blood diverted by the graft and pulmonary arteries, relative to the angle of anastomosis is expressed in Figure 4. It is worth mentioning that among the angles of 30º, 60º and 90º the difference in the percentage of flow which passes through the graft is little changed; for the angle of 110º the flow is greater. However, the distribution of flow by the pulmonary arteries is more uniform at 60º and 90º and it is excessively favored by one or other pulmonary artery at the angles of 30º and 110º.

Fig. 4 - Mean percentage of the flow redirected by the graft and distributed by the pulmonary arteries, in respect to the proximal angle of the anastomosis. There is variability in the distribution of the flow in the pulmonary arteries depending on the angle of the anastomosis
To illustrate the influence of the proximal anastomosis on directed flow to each lung we present in Figure 5 the axial velocity profile at the right and left pulmonary artery outflow tracts of the simulation. It can be seen that for a proximal angle of an anastomosis of 60º the velocity profiles in the pulmonary arteries are practically equal, resulting in a similar blood flow to each of the lungs. A proximal angle of 90º results in very similar profiles. But an anastomosis with an angle of 30º presents a profile with a higher velocity in the right pulmonary artery and lower in the left, whilst in procedures with angles of 110º the opposite occurs.
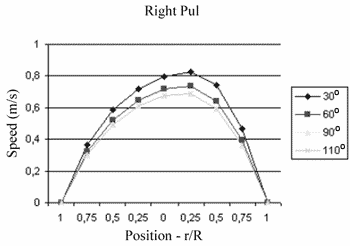
Fig. 5 - Axial velocity profile (m/s) at the right (A) and left (B) pulmonary artery outflow tracts. The position of r/R has reference to the central axis, where the value of 1 presents the central axis of the vessels and the value 0 the internal walls of the analysis. Some simulations were performed with the conditions of defined circuits by Migliavacca et al. [19], with a imposition of established flow in the outflow tract of the subclavian artery
Local analysis of the velocity and pressure fields
Figure 6 presents the velocity profiles along the subclavian artery, the PTFE graft and the pulmonary arteries. Notice that the profile in the subclavian artery tends to become parabolic, although it is not totally developed.

Fig. 6 - Velocity profiles along the geometric model: subclavian artery, PTFE graft and pulmonary branches
There is an influence of the variations of the subclavian artery diameter on the pressure coefficient, as while the section of the subclavian artery is constant, the variation of pressure within it, is close to being linear. This does not occur in variable sections. The near-linear behavior might be justified by "perturbation" to the flow of the subclavian artery caused by the interposition of a tubular graft, diverting part of its flow. There is a very abrupt pressure drop in the region of the anastomosis and after this region there is recovery of the pressure thus creating an adverse pressure gradient, which is a necessary condition for dislocation to occur. In Figure 7, it is possible to verify that the pressure drop is practically the same for the different angles of the proximal anastomosis and for different diameters of the PTFE graft, and it is located at the same point of the subclavian artery.

Fig. 7 - Pressure coefficient (Cp) in the subclavian artery in respect to the angle of the anastomosis (A) and of the diameter of the PTFE graft. It is possible to observe that the pressure drop is very similar to the variations of the angle of the anastomosis and the diameter of the graft
The pressure variations along the PTFE graft vary according to the angle of the anastomosis, as is evidenced in Figure 8. It was observed that for an angle of 30º there is a greater pressure at the proximal anastomosis, which reduces after; with an angle of 110º the pressure along all the route of the graft is low, defining a better flow.
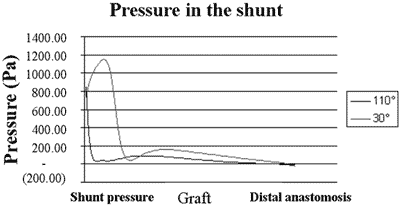
Fig. 8 - Variations in pressure along the PTFE graft depending of the angle of the anastomosis. For an angle of 30º there is a greater pressure near to the proximal anastomosis, reducing afterwards; but an angle of 110º gives low values of pressure in all the route of the graft, defining better flow
The diameter of the graft, as can be seen in Figure 9, has significant importance in the behavior of the flow in the graft and pulmonary artery. As has already been seen, the region of recirculation in the graft increases as the diameter of the graft increases. In relation to the pressure circuits, note that the pressure increases as the diameter of the graft reduces. Nevertheless, the position of the maximum pressure in the graft does not change as the diameter changes.

Fig. 9 - Behavior of the flow in the graft and pulmonary artery according to the diameter of the PTFE graft. Note that the recirculation region in the graft increases as the diameter of the graft increases
Figure 10 presents the lines of current for the anastomosis with angles of 30º and 90º. Notice by the proximal anastomosis, the existence of a region of low velocity with recirculation. The angle of the anastomosis has an influence on the behavior of the flow in this region, which is more favorable at lower angles.


Fig. 10 - Lines of current for anastomosis of 30º and 90º. Near to the proximal anastomosis there is a region of low velocity and with recirculation, where the behavior of the flow in this region is favored by the greater angle of the graft
The occurrence of recirculation in the simulated flows can be studied on graphs of velocity profiles. Note in Figure 11 that the recirculation is little affected with variations in the angle of anastomosis, but suffers influence from the length of the PTFE graft, which is increased by its diameter.

Fig. 11 - Velocity profile, which enables identification of the existence of recirculation in simulated flows. Note that the recirculation is greatly influenced by the diameter of the PTFE graft
DISCUSSION
The geometric complexity, the pulsating nature of flow, the non-Newtonian rheology of the blood and the anisotropic, viscoelastic and non-linear mechanical properties of the arteries are the principal characteristics of the human vascular system which makes its simulation extremely complex to study.
Cole et al. simulated the flow at the bifurcation of the carotid artery, considering the blood as a Newtonian fluid, in a rigid 3-dimensional model, applying the regimes of static flow and subsequently pulsation, utilizing the commercial codes RAMPANT and FLUENT [3]. The results of the performed simulations confirmed the importance of the use of pulsating regimes in arterial blood flow.
Zhao et al. utilized magnetic resonance images of the carotid artery bifurcation to create a computational model with a true vascular anatomy [6]. To perform analyses linking the hemodynamic and mechanical aspects on the arterial wall, the fluid dynamics code CFX4 and the structural mechanics code ABAQUS were employed. The circuit conditions, pressure in the main carotid and the mass flow in the inferior and exterior carotids, were obtained from Doppler echocardiographic examinations. The blood was considered as a Newtonian fluid. The wall thickness of the artery is around 8-10% of the diameter of the vessel and it was assumed to have linear elastic properties. The flows were performed in a rigid model and another dilatable and a quantitative influence on the movement of the artery wall was verified.
PERKTOLD et al. utilized the finite element method of Galerkin to study the blood flow in a pulsating regime at the bifurcation of the left anterior descending coronary artery [21]. The blood was assumed to be a Newtonian fluid, the vessel walls were considered rigid and the conditions of entry were obtained from measurements using Doppler laser. The 3-dimensional geometric model is considered to be very realistic by the authors, characterized by irregularities and flow resistance of the studied artery.
COLE et al. studied the effects of geometric factors in anastomoses performed on the femoral artery [5]. The static and pulsating regimes were applied to a 3-dimensional model, the artery and the graft were assumed to be rigid and the Power Law model was utilized to specify the viscosity of the non-Newtonian flow. The study was motivated by post-surgical complications that occur in this type of procedure; such as the appearance of hyperplasias in the region of the anastomosis.
The advantages of the finite element method is basically due to its high flexibility, which enables us to relatively easily deal with: 1. complicated geometry; 2. generic circuit conditions; 3. materials with non-linear responses and/or with variable properties. It also favors systematization in the development of computational codes. Finally we can highlight the most important advantage of the method: it has a solid mathematical basis, which gives reliability in respect to its codes and, in many problems, makes it possible to establish a priori estimation for the error involved in the approximation of finite elements [22]. On the other hand, if compared with the finite difference method, this flexibility is accompanied with an increase of complexity of programming and a greater quantity of computational memory. The most common finite element method is the one known as the Galerkin Method, which has been applied in the last decades to a vast variety of problems. In this work the finite element stabilized method called "Streamline Upwind/Petrov-Galerkin" (SUPG) was adopted for the problem of advection-diffusion [15-18].
From numeric simulations, it was possible to obtain correlations between the flow deviated by the graft and its diameter, in the range of 4 mm to 6 mm. We can observe that the percentage of flow redirected is greater as the diameter of the graft increases in relation to the subclavian artery. This work confirmed the percentage of flow deviated by the graft as was predicted by Migliavacca et al., which is between 70 and 80% for newborn babies [23].
It was also observed that the angle of proximal anastomosis has a direct influence on the quantity of flow diverted by the graft. This influence starts small for angles between 30º and 60º, situations which correspond to approximately 80% of our sample. Proximal anastomoses with angles of 110º present a greater percentage of deviated flow. This angle, however, has the drawback of excessively increasing the blood flow which reaches the left lung, prejudicing the flow supplied to the right lung. The optimal angle for the proximal anastomosis would be that by which the flow supplied to the two lungs is approximately equal. The simulations performed, indicate that this optimal value, in the majority of the sample group, is between 60º and 90º.
In relation to the distribution and pressure in the graft, the results signal that the location of the pressure peak varies according to the angle of the anastomosis adopted, with an angle of 30º presenting with the highest pressure peak in the implanted graft. As the angle of the anastomosis increases, the highest-pressure region tends to move from the graft to the subclavian artery. This modification might favor thrombosis in the graft due to sanguineous stasis.
As was predicted, the diameter of the graft is the main regulator of the percentage of redirected flow. The greater the diameter, the greater the flow through the graft. But the pressure distribution in the graft is not altered qualitatively by variations in its diameter, with its alterations basically of a quantitative nature.
The study indicates that the utilization of PTFE grafts with diameters greater than that of the subclavian artery are preferable in small children, as they determine a greater redirection of blood to the lungs and because they can maintain this adequate flow with the growth of the patient. The implantation should be at an angle of 60º to 90º in relation to the subclavian artery, aiming to improve the flow pattern and its adequate distribution between the pulmonary arteries. These observations originate from a computerized study and, although supported in publications, they should be proven in clinical trials of operated patients.
ACKNOWLEDGEMENTS
To Dr. Francisco Michielin Filho, who assisted in the collection of data for the construction of the model and in the computerized analysis of the functioning of the Modified Blalock-Taussig Surgery.
BIBLIOGRAPHIC REFERENCES
1. Taylor CA, Hughes TJ, Zarins CK. Finite element modeling of blood flow in arteries. Comput Methods Appl Mech Engin 1998; 158:155-96.
2. Brasil Junior CP, Rosa OLS, Severo CA. Simulação por elementos finitos de escoamento de sangue. In: V Congresso de Engenharia Mecânica Norte e Nordeste; 1998.
3. Cole JS, Gillan MA., Raghunathan SR. A CFD study of steady and pulsatile flows within an arterial bifurcation. In: 36° Aerospace Sciences Meeting & Exhibit, American Institute of Aeronautics and Astronautics; 1998.
4. Asakura T, Karino T. Flow patterns and spatial distribution of atherosclerotic lesions in human coronary arteries. Circ Res 1990; 66:1045-66.
[ Medline ]
5. Cole JS, Gillan MA, Raghunathan SR. Numerical simulations of time-dependent, non-newtonian blood flow through typical human arterial bypass grafts. In: 6° Irish Chemical engineering Research Symposium Cork; 1998. Republic of Ireland.
6. Zhao SZ, Xu XY, Hughes AD, Thom SA, Stanton AV, Ariff B et al. Blood flow and vessel mechanics in a physiologically realistic model of a human carotid arterial bifurcation. J Biomech 2000; 33: 975-84.
[ Medline ]
7. deLeval MR, McKay R, Jones M, Stark J, Macartney FJ. Modified Blalock-Taussig shunt: use of subclavian artery orifice as flow regulator in prosthetic systemic-pulmonary artery shunts. J Thorac Cardiovasc Surg 1981; 81:112-9.
8. Blalock A, Taussig HB. Surgical treatment of malformations of the heart in which there is pulmonary stenosis or pulmonary atresia. JAMA 1945; 128: 189-202.
9. Neches WH, Naifeh JG, Park SC, Lenox CC, Zuberbuhler JR, Siewers RD et al. Systemic-pulmonary artery anastomoses in infancy. J Thorac Cardiovasc Surg 1975; 70: 921-7.
[ Medline ]
10. Odim J, Portzky M, Zurakowski D, Wernovsky G, Burke RP, Mayer Jr. JE et al. Sternotomy approach for the modified Blalock- Taussing shunt. Circulation 1995; 92(9 suppl): II256-61.
11. Thomé GL. Cirurgia de Blalock-Taussig modificada com prótese de politetrafluoretileno: resultados imediatos e tardios [Tese de mestrado]. Porto Alegre: Fundação Universitária de Cardiologia, 1993.
12. Pennati G, Fiore GB, Migliavacca F, Lagana K, Fumero R, Dubini G. In vitro steady-flow analysis of systemic-to-pulmonary shunt haemodynamics. J Biomech 2001; 34: 23-30.
[ Medline ]
13. Nesralla IA. Cardiologia cirúrgica: perspectivas para o ano 2000.1a ed. São Paulo: Fundo Editorial Byk-Procienx. p.110.
14. Hughes TJR, Liu W, Brooks AN. Finite element analysis of incompressible viscous flows by the penalty function formulation. J Comput Physics 1979; 30:1-60.
15. Hughes TJ, Brooks NA. Finite element methods for convection dominated flows. 2a ed. New York: ASME;1979. p.19-35.
16. Hughes TJR, Franca LP, Balestra M. A new finite element formulation for computational fluid dynamics: V. Circumventing the Babuska-Brezzi condition: A stable Petrov-Galerkin formulation of the Stokes problem accomodating equal-order interpolations. Comput Methods Appl Mech Eng 1986; 59: 85-99.
17. Hughes TJR, Mallet M, Franca LP. Entropy-stable finite element methods for compressible fluids: application to high order Mach number flow with shocks. Finite element methods for nonlinear problems 1986; 121:761-73.
18. Vawter DL. Possion´s ratio and incompressibility. J Biomech Eng 1983; 105:194-5.
19. Migliavacca F, Dubini G, Pennati G, Pietrabissa R, Fumero R, Hsia TV, de Leval MR. Computational model of the fluid dynamics in systemic-to-pulmonary shunts. J Biomech 2000; 33:549-57.
[ Medline ]
20. Thomas LH. Elliptic problems in linear dufference equations over a Network. New York: Watson Sci. Comput. Lab. Report, 1972.
21. Perktold K, Hofer M, Rappitsch G, Loew M, Kuban BD, Friedman MH. Validated computation of physiologic flow in a realistic coronary artery branch. J Biomech 1998; 31: 217-28.
[ Medline ]
22. Malkus DS, Hughes TJR. Mixed finite element methods - reduced and selective integration techniques: a unification of concepts. Comput Methods Applied Mech Eng 1978; 15:63-81.
23. Migliavacca F, Yates R, Pennati G, Dubini G, Fumero R, de Leval MR. Calculating blood flow from doppler measurements in the systemic-to-pulmonary artery shunt after the Norwood operation: a method based on computational fluid dynamics. Ultrasound Med Biol 2000; 26: 209-19.
[ Medline ]













 All scientific articles published at bjcvs.org are licensed under a Creative Commons license
All scientific articles published at bjcvs.org are licensed under a Creative Commons license